FDTD法
どんなもの？

　この数値計算法では、Maxwell方程式 を離散化して差分計算を行っている。単位時間毎に計算結果が出るので、時間領域で電磁界解析場合には非常に有効な手法である。
　しかし、計算結果に差分誤差を含んでいるので、他の数値計算法に比べると精度はイマイチである。また、解析空間を格子状にカットして各点に対して計算をしているのでメモリを多く消費する。

どんなかんじなの？～二次元問題～

↑このように解析領域の中に完全導体を置いた場合の電磁波伝搬の様子。

FDTD法を用いると電磁波の散乱の様子が時間領域で解析することができる。

遠方界

「物体に電波を当てたとき、どんな方向に散乱するんだろう？」
「アンテナから出た電波はどんな方向に飛んでいくんだろう？」

ということを議論するとき、

"遠方界"

という世界で電磁波がどんな振る舞いをするかということを考える。

えんぽうかいってなに？

　電磁波の伝搬の振る舞いを考えるとき、 "波長"という長さを基本単位とする。電磁波の発生源から波長程度の距離の領域を近傍界、波長に比べ十分に長い距離の領域を遠方界とそれぞれ呼ばれている。また、電磁波を情報伝送の手段と考えたとき、送受信間の距離は波長に比べて十分長いので、遠方界で電波伝搬を考えている。

計算のしかた

　FDTD法を普通に用いると遠方までの各点を毎回毎回計算しなくてはならなくなり、膨大な計算時間、メモリを消費することになる。そこで、近傍の電磁界から遠方を推定し、無駄な計算をしないようにする。
　近傍から遠方を推定するには、等価定理や様々な数式を用いて変形させる。

等価定理って？

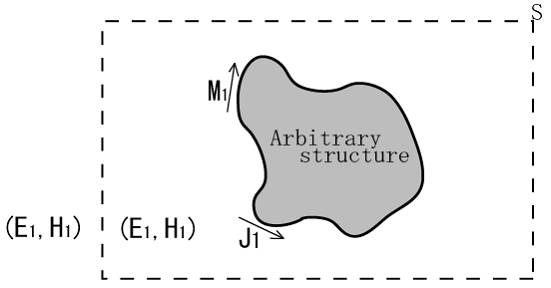
　このように任意構造物を波源（一次波源）としたとき、それを取り囲むように閉曲面を考える。

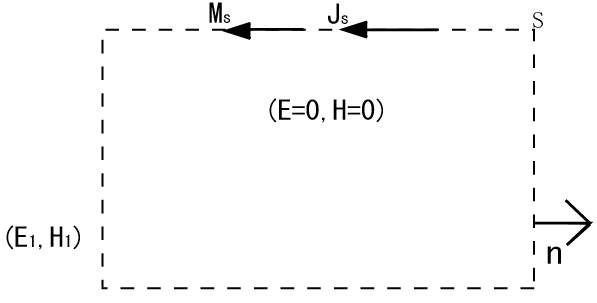
　閉曲面内の電磁界を0としたとき、境界条件より閉曲面上を流れる電磁流を波源（二次波源）とみなし、そこからの放射を考える。これにより、本当の波源を知らなくても遠方界が算出できる。

指向性図

　等価定理などを行い算出した遠方界をグラフで表したものは指向性図と呼ばれ、アンテナなどの性能を評価するのに使用される。

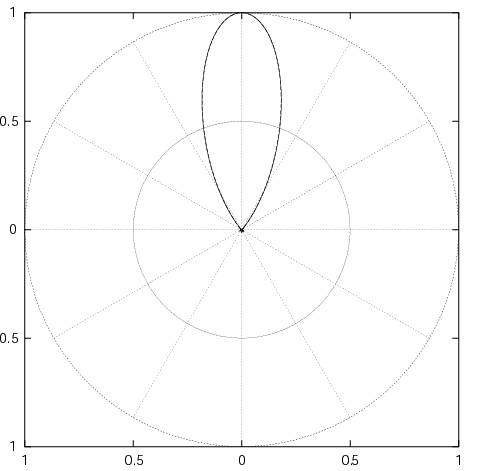
↑8素子の八木アンテナの指向性を解析した結果

FDTD法 どんなもの？